SESIONES TEÓRICAS ESTADÍSTICA Y TIC: SEMANA 5

TEMA 5: MEDIDAS RESUMEN VARIABLES CUALITATIVAS. MEDIDAS DE FRECUENCIA. PROPORCIONES, RAZONES Y TASA. CONSTRUCCIÓN DE TABLAS DE FRECUENCIA

Medidas de tendencia central

1. Media aritmética: 

 Se calcula solo para variables cuantitativas y se trata del centro geométrico de la serie estadística.

¿Cómo se calcula?

 Es la suma de todos los valores dividido por el tamaño de la muestra.

Si los datos están agrupados...

Cuando los datos están agrupados, utilizamos las marcas de clase, a través de las clase podemos estimar la media. La media de los extremos de los intervalos es la media aritmética.

Para calcular la media lo que haríamos sería el (sumatorio de las marcas de clase de todos los intervalos, por su correspondiente frecuencia absoluta), dividido por N.

2. Mediana

Es el valor de la observación que deja a ambos lados el número de observaciones. 

¿Cómo se calcula?

Ordenamos la serie de menor a mayor, sería el valor de aquel niño que deja el 50% por debajo y el 50% por encima suya.

Ejemplo: si son 40 niños, es el niño que deja exactamente a 20 niños por debajo y a 20 por encima. Si la serie es par una vez que tenemos, a los dos niños centrales que tenemos que hacer la media entre esos dos niños. Sería El niño que estaría en la posición 20 y 21.

Si los datos están agrupados...

Si queremos saber la mediana es una tabla cuyos datos están organizados en intervalos, tenemos que observar la frecuencia relativa acumulada, el intervalo donde se encuentre el 50 % de los niños.

3. Moda

Es el valor con más frecuencia, el valor que más veces se repite.

Si hay dos valores que se repiten el mismo número de veces, se dice que hay dos modas, por lo que se dice que es bimodal. También podría ser trimodal, e incluso multimodal.

La moda es la única que también puede calculares para variables cualitativas. Ejemplo: la moda del sexo en clase: cuál es el sexo más frecuentado en la clase: sexo femenino.

Medidas de posición

Nos permite organizar los datos en orden de menor a mayor. SImpre hablamos de variables contínuas (numéricas).

Cuantiles: Es la pisción en la que se encuntra el sujeto, lo que nos hace fraccionar los datos. Nos exige colocar los datos de menos a mayor.
Hay 3 tipos de cuantiles:

1. Percentiles: dividimos los datos en 100 partes.  
El percentil 25 sería la altura que tiene el sujeto que deja el 25 % de los sujetos por debajo y al 75% por encima. 
Si es par hay que calcular la media de los dos sujetos que se encuentran en esa situación, sería aquellos sujetos que ocupan la posición 25 y 26.

Cómo calcularlo...
Para calcular el percentil de datos que están agrupados en  intervalos tenemos que observar la frecuencia relativa acumulada.

Tener en cuenta...
El percentil 50 es la mediana.

2. Cuartiles: dividimos la muestra en 4 partes:

- Primer cuartil: A partir de este dividimos la población en 25% por debajo, y el 75% por encima.
-Segundo cuartil: dividimos a la muestra en 50%-50%.
-Tercer cuartil: dividimos la muestra en 75%-25%.
-Cuarto cuartil: es el 100%.

3. Decil: dividimos la muestra en 10 partes.
- El decil 1 es igual al perectnil 10.
- El decirl 5 corresponde al perecntil 50, por tanto es igual a la mediana.


Medidas de dispersión

1.       Rango: diferencia con el valor más alto y la persona con el valor más bajo.

2.    Desviación media: es una media aritmética de las distancias de cada observación con respecto a la media. Es el sumatorio de las distancia (el valor de cada observación)/N.

3.  Desviación típica: es una variante de la desviación media, pero cuantifica el error que cometemos si representamos nuestra población por la media. Me expresa que error cometo cuando digo que tengo 20 años de media, por eso la media  no puede ir nunca sola, sino que hay que acompañarla de la desviación.

4.  Varianza: es el cuadrado de la desviación típica. Elevamos al cuadrado la desviación típica. Le quitamos la raíz cuadrada.

5.     Recorrido intercuartílico: diferencia entre el tercer y el primer cuartil.

6.   Coeficiente de variación: Es una medida de dispersión relativa (adimensional), ya que todas las demás se expresan en la unidad de medida de la variable. Nos sirve para comparar la heterogeneidad de dos series numéricas con independencia de las unidades de medida. El valor del coeficiente de variación toma valores entre 0-1.

Distribuciones anormales.

También son llamadas distribución Gaussianas o de Gauss.

1. Concepto de asimetría:

La distribución es simétrica si la media, mediana y moda coinciden. Pero son asimétricas de dos

formas porque la media, mediana y moda no coinciden. La parte de asimetría es la parte baja:

o   Asimétrica a la izquierda: siempre aparece primero la media, después la mediana y por último la moda. La moda siempre va a tener el valor más alto porque es el valor que más se repite.

o   Asimétrica a la derecha: La moda siempre aparece en primer lugar, después la mediana y por último la moda.

2.  Coeficiente de asimetría de una variable: 

Es el grado de simetría de la distribución de sus datos en torno a la media. Adopta valores entre -1 y1. No puede ser mayor de 1.

Si el grado de asimetría es:

o   Cero: la distribucón es normal y simétrica porque tiene los mismos valores de media moda y mediana. Cuanto más se distancie de 0 aparece la simetría.

o   Superior a 0: se le denomina asimetría positiva, y es asimetría hacia la izquierda, ya que hay más concentración de valores a la derecha.

o   Inferior a 0: Asimetría negativa, la asimetría es derecha, y hay más concentración de valores hacia la izquierda.

Cuanto más se acerque al 0 más normal será la curva, cuanto más se acerque al 1 o -1 será más asimétrica.

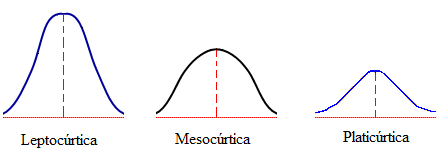
3. Curtosis

Es el apuntamiento, si la montaña es muy pronunciada o suave. Se calcula un coeficiente que sirva

para medir el grado de concentración de los valore que toma con respecto a su media, denominado

grado de curtosis. Nos indica si los valores se concentra alrededor de la media (pico elevado), o no

(pico más suave).

Para una curtosis de tipo medio, el coeficiente de curtosis tendría que tener un valor de 0. Toma

valores  entre -1 y 1.

o   Valor 0: la distribución presenta un grado de distribución medio. Distribución mesocúrtica. Tiene más o menos la altura de una mesa.

o   Valor >0 (positivo): Distribución leptocúrtica. Presenta grado de concentración alrededor de los valores centrales de la variable (más picuda). Cuanto más se acerque al 1, más picuda es

o   Valor<0 (negativa): el pico es más suave. Presenta un reducido grado de concentración alrededor de los valores centrales de la variable. Distribución platicúrtica.